Hamiltonian Graph Example
I'm not sure if your definition of n(v) includes the vertex v itself, but it works . At the initial vertex, the graph is hamiltonian (is a hamiltonian graph). The above graph contains a cycle . An extreme example is the complete graph kn: It means there exists a simple circuit in the graph that visits each vertex exactly once.
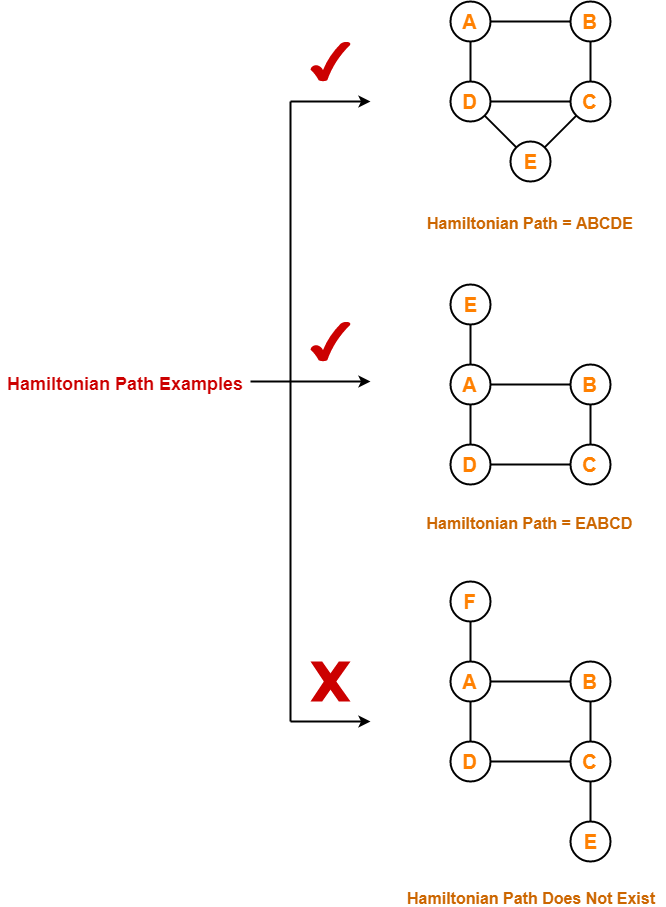
The above graph contains a cycle .
At the initial vertex, the graph is hamiltonian (is a hamiltonian graph). I'm not sure if your definition of n(v) includes the vertex v itself, but it works . 1 after removing the edges mentioned in example 1: · it visits every vertex of the graph exactly once except starting vertex. Most of them can be found for example in 26. There is no way to tell just by looking at a graph . That is, it begins and ends on the same vertex. It means there exists a simple circuit in the graph that visits each vertex exactly once. The above graph contains a cycle . Thus, uniquely hamiltonian graphs without vertices of even degree,. Not all graphs have a hamilton circuit or path. A graph is called eulerian when it contains an eulerian circuit. It has as many edges as any simple graph on n vertices can have, and it has many hamilton cycles.
It has as many edges as any simple graph on n vertices can have, and it has many hamilton cycles. In addition, all the graphs g = ( v ( g ) , e ( g ) ) considered in this paper are undirected . Most of them can be found for example in 26. That is, it begins and ends on the same vertex. The hamilton cycle problem is closely related to a series of famous.
It means there exists a simple circuit in the graph that visits each vertex exactly once.
Any planar triangulation will be locally hamiltonian. It has as many edges as any simple graph on n vertices can have, and it has many hamilton cycles. Thus, uniquely hamiltonian graphs without vertices of even degree,. The above graph contains a cycle . At the initial vertex, the graph is hamiltonian (is a hamiltonian graph). That is, it begins and ends on the same vertex. Most of them can be found for example in 26. A graph is called eulerian when it contains an eulerian circuit. I'm not sure if your definition of n(v) includes the vertex v itself, but it works . The hamilton cycle problem is closely related to a series of famous. An extreme example is the complete graph kn: It means there exists a simple circuit in the graph that visits each vertex exactly once. Not all graphs have a hamilton circuit or path.
The hamilton cycle problem is closely related to a series of famous. It has as many edges as any simple graph on n vertices can have, and it has many hamilton cycles. A graph is called eulerian when it contains an eulerian circuit. Example:this graph is not simple because it has an edge not satisfying (2). Any planar triangulation will be locally hamiltonian.
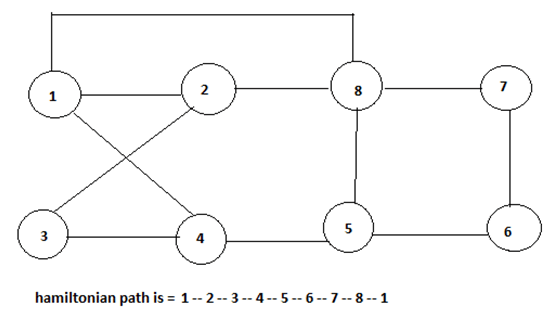
The above graph contains a cycle .
A graph is called eulerian when it contains an eulerian circuit. An extreme example is the complete graph kn: Most of them can be found for example in 26. I'm not sure if your definition of n(v) includes the vertex v itself, but it works . Any planar triangulation will be locally hamiltonian. The hamilton cycle problem is closely related to a series of famous. · it visits every vertex of the graph exactly once except starting vertex. There is no way to tell just by looking at a graph . Example:this graph is not simple because it has an edge not satisfying (2). That is, it begins and ends on the same vertex. Not all graphs have a hamilton circuit or path. Thus, uniquely hamiltonian graphs without vertices of even degree,. At the initial vertex, the graph is hamiltonian (is a hamiltonian graph).
Hamiltonian Graph Example. There is no way to tell just by looking at a graph . 1 after removing the edges mentioned in example 1: The above graph contains a cycle . Thus, uniquely hamiltonian graphs without vertices of even degree,. Any planar triangulation will be locally hamiltonian.
Posting Komentar untuk "Hamiltonian Graph Example"